In this year, I have read a lot of blockchain related articles and many friends asking how to study blockchain especially on the first half of 2018 :). Thus I am going to note down what I learned and introduce my path of learning blockchain and DApp developement.
Basic Question

Figure 1. Blockchain Layers
-
What is Blockchain?
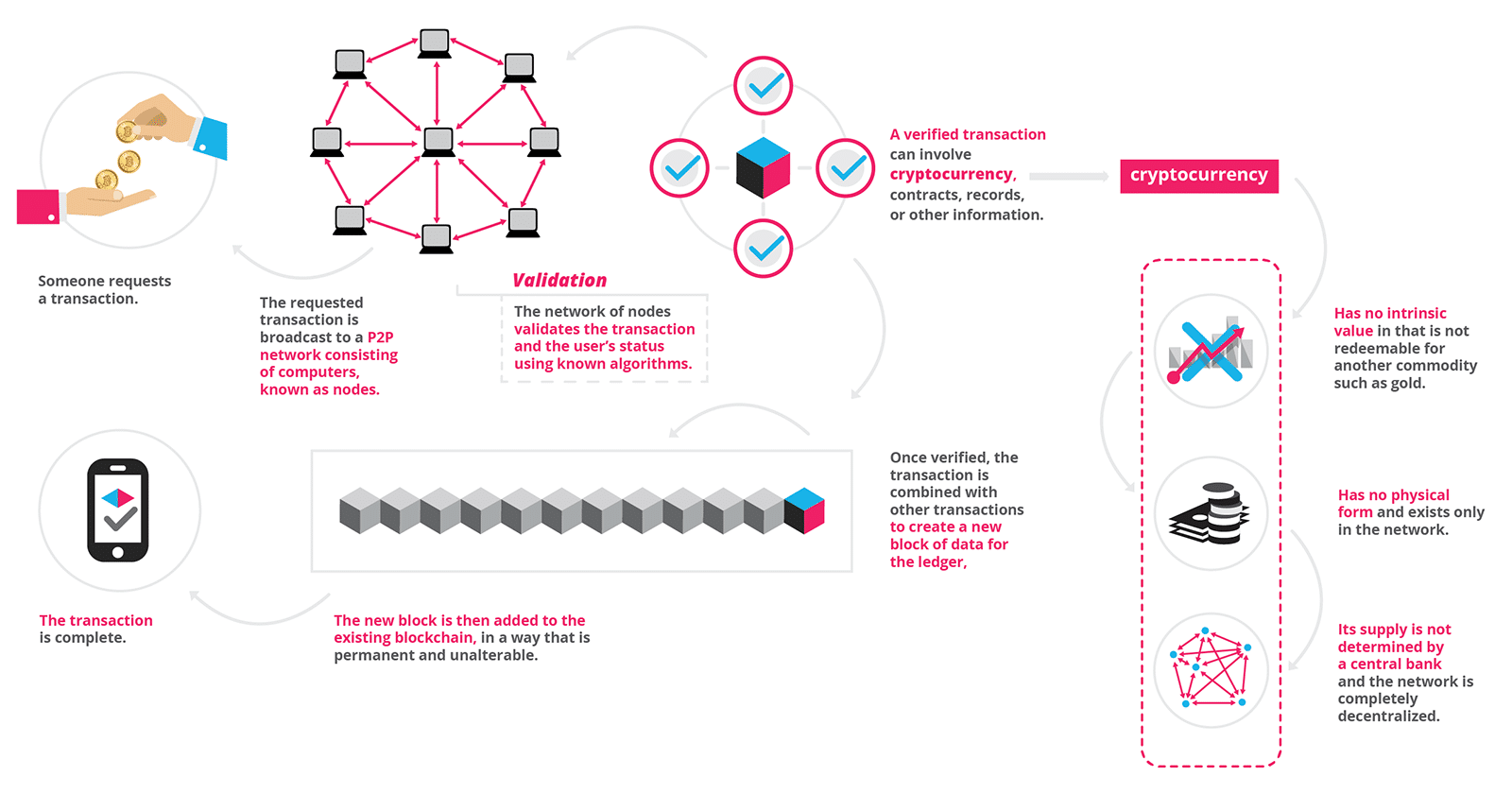
Figure 2. Blockchain features
Blockchain is a smart peer-to-peer network that uses distributed database technology to identify, propagate, and record information.
The blockchain records information in a decentralized manner so that the information is not changeable and does not require any central review.
Blockchain is not a single technology, but the result of multiple technology integrations. Including: asymmetric encryption, hash algorithm, digit signature, peer-to-peer network transmission technology and consensus mechanism.
The block is the account page and the blockchain is the ledger. From this, you can calculate the balance of all accounts, so that all participants’ ability to pay at a glance, so as to eliminate any possibility of double spending. Previously, the process of recording, storage, inspection, and validation required participation by third parties, such as banks.
1) Each transaction is digitally signed using the currency owner’s private key.
2) All transactions in each time period are packaged together. This package is called a block.
3) Through the hash algorithm, hash the transaction record and packing each block into the next block, and all blocks are connected in series, which is the blockchain.
BTC Block

Figure 3. BTC block header and body
Figure 4. Block Header data structure
classBlock {
public index:number;
public hash:string;
public previousHash:string;
public timestamp:number;
public data:string;
public difficulty:number;
public nonce:number;
constructor(index:number, hash:string, previousHash:string,
timestamp:number, data:string, difficulty:number, nonce:number) {
this.index=index;
this.previousHash=previousHash;
this.timestamp=timestamp;
this.data=data;
this.hash=hash;
this.difficulty=difficulty;
this.nonce=nonce;
}
}
PrevBlock
The PrevBlock is the ID of the previous block of the current block. It is precisely because the current block is generated based on the ID of the previous block.
Here, the “block header information” is the string formed by the last block of the current block “PrevBlock + MerkleRoot + Nonce + Time + Bits…”; the SHA256 function is a hashing function. Obviously, PrevBlock is known for the current block.
Merkle Tree
It consists of a root node (root), a set of intermediate nodes, and a set of leaf nodes. A leaf node contains stored data or its hash value. The intermediate node is the hash value of its two child node contents. The root node is also composed of the hash values of its two child node contents. So the Merkle tree is also called the hash tree.
The leaf node stores the data file, and the non-leaf node stores the hash value of its child nodes (Hash, calculated by hash algorithm such as SHA1, SHA256, etc.). The hash of these non-leaf nodes is called hash path. The value (which can be used to determine the path from a leaf node to the root node), and the hash value of the leaf node is the hash value of the real data. Because of the tree structure, the time complexity of the query is O(logn), and n is the number of nodes.
The hash value of the leaf node is the hash value of the real data. Because of the tree structure, the time complexity of the query is O(logn), and n is the number of nodes.
Any changes to the underlying data are passed to its parent node up to the root of the tree.
Typical application scenarios for the Merkel tree include:
1. Quickly compare large amounts of data: When two Merkel roots are the same, it means that the data represented must be the same (determined by the hash algorithm).
2. Quick positioning modification: For example, in Figure 3, if the data in Tx1 is modified, it will affect Hash0, Hash01 and Root. Therefore, along Root –> Hash01 –> Hash0, you can quickly locate the changed Tx1;
Zero-knowledge proof: For example, how to prove that a certain data (D0…D3) includes a given content D0 is very simple. Construct a Merkel tree and publish N0, N1, N4, Root, and D0 owners can easily detect D0. Exist, but don’t know anything else.
Compared with the Hash List, the obvious advantage of Merkle Tree is that it can take a single branch (as a small tree) to verify part of the data. This many use cases bring convenience to the hash list. Efficient. It is from these advantages that Merkle Tree is often used in distributed systems or distributed storage.
In order to keep the data consistent, the data between the distributed systems needs to be synchronized. If all the data on the machine are compared, the amount of data transmission will be large, resulting in “network congestion.” To solve this problem, you can construct a Merkle on each machine. In this way, when the data is compared between the two machines, the comparison is started from the root node of the Merkle Tree. If the root node is the same, it means that the two copies are currently consistent and no longer need any processing; if not Then, the query is performed along the node path with different hash values, and the leaf nodes with inconsistent data can be quickly located, and only the inconsistent data can be synchronized, which greatly saves the comparison time and the data transmission amount.
The bitcoin blockchain system uses the Merkle binary tree, which is mainly used to quickly summarize and verify the integrity of the block data. It will hash the data packets in the blockchain and continuously recursively upward. A new hash node is generated, and finally only one Merkle root is stored in the block header, and each hash node always contains two adjacent data blocks or their hash values.
There are many advantages to using a Merkle tree in a Bitcoin system: first, it greatly improves the efficiency and scalability of the blockchain, so that the block header only needs to contain the root hash value without having to encapsulate all the underlying data, which makes the hash The operation can run efficiently on smartphones and even IoT devices; secondly, the Merkle tree supports the Simplified Payment Verification Protocol (SPV), which allows transaction data to be executed without running a full blockchain network node. test. Therefore, it is very meaningful to use a data structure such as a Merkle tree in a blockchain.
SPV (Simplified Payment Verification): A method for verifying payment easily and securely even without a complete transaction record. Instead of downloading all the blocks (several hundred G), you can easily verify all payments by simply downloading all the block headers (about 40M).
The block header is the identity information of the block, and contains a special hash value – Merkle Tree Root
The miners lined up the hashes of all the transactions in the block (about 1-2 thousand pens), letting them hold hands in pairs, and each pair of trades hand in hand to calculate a new hash. The process by which miners verify, record, and organize transactions is called “packaging.”
A hash of the Merkel root contains all transaction validation information within the block.
Please note: it is transaction verification information, not transaction information. To query specific transaction information, you have to download the full node block data; but verify that a transaction is recorded, download block header data is sufficient, because there is a simple payment verification (SPV) method.
How many SPV methods can you see?
The block confirms this transaction and can be considered absolutely reliable if it is confirmed by more than 6 blocks (6 is a reliable empirical value).
Difficulty & Bits
There are similar rules in the Bitcoin protocol. Satoshi Nakamoto first defined a 64-bit hexadecimal integer 0x00000000FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF (the first two digits 0x represent hexadecimal), the condition of the whole network computing power at that time. Next, a hash of about 10 minutes will find a number less than or equal to this integer. As the creator, it is stipulated that the time at which the whole network has the computing power to find that number is 1; the subsequent use of this standard, based on the changing network power, dynamically adjusts a matching and proportional Difficulty The difficulty value is to ensure that the 10-minute operation of the whole network can find the number that meets the requirements. The adjustment period is about once every two weeks, that is, the Difficulty value is adjusted once every 2016 block is dug out.
Bits is another form of data representation corresponding to Difficulty. The two essentially express the same purpose, but the process of conversion is a bit complicated, and there is no need to tangled. All you need to know is that Difficulty & Bits is easy to know when the entire network is fixedly known.
Nonce
Time
Approximate timestamp generated by the current block. Why do you say “approximation”? This is because in a decentralized blockchain world, this timestamp is calculated by averaging the timestamps of the other nodes associated with the block node, not exactly equivalent to international standards. This value is obviously also fixedly known.
The above are some of the data fields that I think are more important in the block header. If you have a basic understanding of the above terms, we can finally continue to the next step – to explore the mathematical essence of “mining”:
Step1: Calculate a new Target target value according to the following formula
Among them, a certain constant is the 64-bit hexadecimal integer 0x00000000FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF, which we said earlier. When Bitcoin was created, Difficulty was 1, and it has been dynamically adjusted according to the periodicity of the whole network for many years. Difficulty.
In the existing algorithm, the solution of the current Target value does not need to execute the above calculation formula every time. The actual algorithm is directly solved according to the Target value of the previous block. The effect calculated by the two is actually it’s the same:


Mining

Figure 5. Mining Difficulty
-
BLOCK_GENERATION_INTERVAL, defines how often a block should be found. (in Bitcoin this value is 10 minutes)
-
DIFFICULTY_ADJUSTMENT_INTERVAL, defines how often the difficulty should adjust to the increasing or decreasing network hash rate. (in Bitcoin this value is 2016 blocks)

Figure 6. Mining Height Difficulty
Digital Signature
Hash
Cryptography
Symmetric Cryptography
Encrypt and decrypt with the same key
The advantage of symmetric encryption is that the encryption and decryption efficiency is high (fast speed, small space occupation), and the encryption strength is high.
The disadvantage is that all parties involved need to hold the key. Once someone leaks, the security is destroyed. How to distribute the key under the insecure channel is a key issue.
Encryption process: original + key = “cipher-text”; decryption process: cipher-text + key = original.
Symmetrical passwords can be divided into two types: block ciphers and sequence ciphers.
The former divides the plaintext into fixed-length data blocks as the encryption unit, which is the most widely used.
The latter encrypts only one byte, and the password is constantly changing, only used in certain areas, such as digital media encryption.
Asymmetric cryptography
Asymmetric encryption is the greatest invention in the history of modern cryptography, and it can solve the problem of early distribution of keys needed for symmetric encryption.
The encryption key and the decryption key are different and are called public and private keys, respectively.
The public key is generally public and accessible to everyone. The private key is generally held by the individual and cannot be obtained by others.
The public key is used for encryption and the private key is used for decryption.
The public key is generated by the private key, the private key can derive the public key, and the private key cannot be derived from the public key.
The advantage is that the public and private keys are separated and unsafe channels can be used. The disadvantage is that the encryption and decryption speed is slow, generally 2 to 3 orders of magnitude slower than the symmetric encryption and decryption algorithm; at the same time, the encryption strength is worse than symmetric encryption.
Encryption process: original + recipient public key = cipher-text; decryption process: cipher-text + recipient private key = “original
Generally applicable to signature scenarios or key negotiation, not suitable for encryption and decryption of large amounts of data. Among them, the RSA algorithm has been considered to be not safe enough, and an elliptic curve series algorithm is generally recommended.
1) RSA
Four steps to set the key (public and private):
1. Find two prime numbers P and Q, multiply P and Q to get Max, ie Max = P × Q
2. Decrease the two prime numbers by one and multiply them to get M, ie M = (P‐1) × (Q1)
3. Find a positive integer E to make E and M mutually prime, and E<M
4, find a positive integer D, so that D × E divided by M remaining 1, that is (D × E) mod M = 1
E is the public key. Encryption is to let the original text multiply (E‐1) times and get the cipher text.
D is the private key. Decryption means that the cipher text is self-multiplied (D-1) times and the original text is obtained.
The only way to crack the private key is to decompose P and Q from Max.
It is easy to push backwards. This is Trapdoor Function, which is the basis of asymmetric cryptographic security.
Some algorithms have been able to split a specific large number, so for security, people will use a larger prime number, but in this way, the key length will be lengthened, eventually slowing down the encryption and decryption speed. The user is in a dilemma: it is not convenient to lengthen the key, not to lengthen the key.
2) Elliptic Curve Cryptography (ECC)
Y^2 = x^3 + ax + b
Let’s choose a little kickoff on the elliptical curve.
1. The billiard ball hits B, bounces to another intersection, and then bends to the intersection point and the symmetry point C of the x-axis;
2. After going to C, it will bounce to A. When passing the curve intersection point, the ball will turn to the symmetry point D of the intersection point;
3. After D, it will follow the AD direction, and shoot at another intersection of the curve and the line, and then bounce to the symmetry point E of the intersection;
The number of hits n is your private key, a super large integer of your choice; the billiard hits n times to stop, and the coordinates of the end point is equivalent to the public key; if you want to make another public key, then change the coordinates of the starting point.
The elliptic curve equation, the starting point and the end point coordinates are completely open, but the calculation of the ball hits several times before stopping, but there is no shortcut, only have to test. It is more difficult than the task of splitting Max in RSA, which is why ECC is safer than RSA.
Bitcoin, also uses ECC’s digital signature algorithm ECDSA (Elliptic Curve Digital Signature Algorithm), not only the security performance is good, but the ECDSA signing name is two orders of magnitude faster than the RSA signature.
Second, you can sign a specific message by sk: sig:= sign(sk, message) so that you get the specific signature sig
Finally, the party that owns the signed public key can verify the signature: isValid := verify(pk, message, sig)
In the blockchain system, each data transaction needs to be signed. In the design process of the bitcoin, the user’s public key is directly used to characterize the user’s bitcoin address.
In this way, when the user initiates a bitcoin transaction such as transfer, the legality verification of the user transaction can be conveniently performed.

Figure 7 Digit Signature by ECDSA
Details of Transaction Digital Signature

Figure 8. Digital Signature
-
Hash function (SHA256) for the Proof-of-work mining (The hash is also used to preserve block integrity)
-
Public-key cryptography (ECDSA) for transactions

Figure 9. Transaction of the block
classTxOut {
public address:string;
public amount:number;
constructor(address:string, amount:number) {
this.address=address;
this.amount=amount;
}
}
classTxIn {
public txOutId:string;
public txOutIndex:number;
public signature:string;
}

Figure 10. Transaction in/output
class Transaction {
public id:string;
public txIns:TxIn[];
public txOuts:TxOut[];
}