Hi Guys,
Today, let’s talk about the GMM (Gaussian Mixture Model) and how to use the GMM in scikit learn and Spark.
I. Background Knowledge
Maximum-likelihood estimation (MLE) is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model’s parameters.
Expectation–maximization (EM) algorithm is an iterative method for finding maximum likelihood, where the model depends on unobserved latent variables. The EM iteration alternates between performing an expectation (E) step, which creates a function for the expectation of the log-likelihood evaluated using the current estimate for the parameters, and a maximization (M) step, which computes parameters maximizing the expected log-likelihood found on the Estep. These parameter-estimates are then used to determine the distribution of the latent variables in the next E step.
GMM:
1. Objective function:§Maximize the log-likelihood and using EM as framework
2. EM algorithm:
E-step: Compute posterior probability of membership.
M-step: Optimize parameters.
Perform soft assignment during E-step.
Here’s a good youtube tutorial to tell the difference between K-means, GMM and EM.
Some definitions and terms from wiki
1.
N random variables corresponding to
observations, each assumed to be distributed according to a mixture of
K components, with each component belonging to the same
parametric family of distributions (e.g., all
normal, all
Zipfian, etc.) but with different parameters
3. Normal distribution (
Gaussian distribution) . Notation is

, where
μ ∈ R — mean (
location)
σ2 > 0 — variance (squared
scale). Therefore, if the GMM model returns
μ and
σ2, we can plot the mixed distribution functions.
II. Mathematics Proof
Here are the very detailed and relatively easy to understand videos illustrate GMM and EM algorithms
GMM
EM-part1
EM_part2
EM_part3
EM_part4
II. IPython Code (Github)
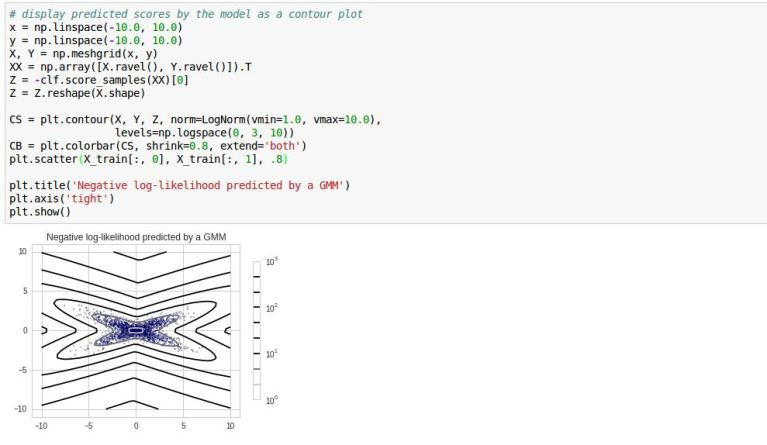
The following contour plot image indicates the envelope of two GMM components distributions
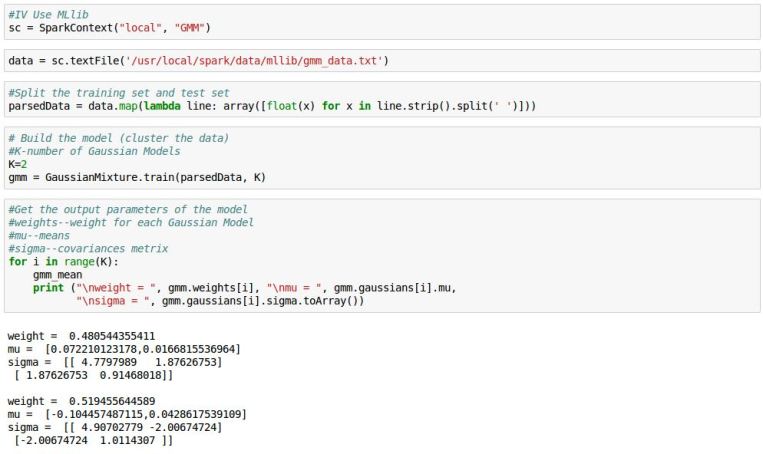
The following Code is based on PySpark
We can see both of scikit-learn and pyspark model indicates similar GMM components mixture.
Reference
1. http://blog.csdn.net/zouxy09/article/details/8537620 (in Chinese)
2. http://stackoverflow.com/questions/23546349/loading-text-file-containing-both-float-and-string-using-numpy-loadtxt
3. https://spark.apache.org/docs/latest/mllib-clustering.html#latent-dirichlet-allocation-lda
4. http://scikit-learn.org/stable/auto_examples/mixture/plot_gmm_pdf.html#example-mixture-plot-gmm-pdf-py
5. https://github.com/apache/spark/blob/master/data/mllib/gmm_data.txt
6. https://en.wikipedia.org/wiki/Mixture_model#Gaussian_mixture_model
 , where μ ∈ R — mean (location)
, where μ ∈ R — mean (location)